 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( ) 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )A. | B. |
C. | D. |
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
| A.平均数 | B.众数 | C.方差 | D.中位数 |
| A.有实数根 | B.有两个不相等的实数根 |
| C.有两个相等的实数根 | D.以上说法都不对 |

| A.25° | B.40° | C.80° | D.100° |
 ,那么函数y=2★x的图象大致是( )
,那么函数y=2★x的图象大致是( )A. | B. | C. | D. |
 【题文】函数y=
【题文】函数y= 中自变量x的取值范围是_____.【题文】如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为
中自变量x的取值范围是_____.【题文】如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为 【题文】若方程组
【题文】若方程组 的解是
的解是 ,则b=_____.【题文】如图,AB是半圆O的直径,且AB=6cm,点C为半圆上的一点,将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是_____.
,则b=_____.【题文】如图,AB是半圆O的直径,且AB=6cm,点C为半圆上的一点,将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是_____. 【题文】如图图形都是由同样大小的正方形“□”按照一定规律排列的,其中图①中共有2个正方形,图②中共有4个正方形,图③中共有7个正方形,图④中共有12个正方形,图⑤中共有21个正方形,……,照此规律排列下去,则图⑩中正方形的个数为_____.
【题文】如图图形都是由同样大小的正方形“□”按照一定规律排列的,其中图①中共有2个正方形,图②中共有4个正方形,图③中共有7个正方形,图④中共有12个正方形,图⑤中共有21个正方形,……,照此规律排列下去,则图⑩中正方形的个数为_____. 【题文】计算:
【题文】计算: .【题文】已知2a2+3a-6=0.求代数式3a(2a+1)-(2a+1)(2a-1)的值.【题文】陈钢和王昊两人从甲市开车前往乙市,甲、乙两市的行驶路程为180千米.已知王昊行驶速度是陈钢行驶速度的1.5倍,若陈钢比王昊早出发0.5小时,结果陈钢比王昊晚到0.5小时,求陈钢、王昊两人的行驶速度.【题文】如图,在△ABC中,AB=AC,点M在BA的延长线上.
.【题文】已知2a2+3a-6=0.求代数式3a(2a+1)-(2a+1)(2a-1)的值.【题文】陈钢和王昊两人从甲市开车前往乙市,甲、乙两市的行驶路程为180千米.已知王昊行驶速度是陈钢行驶速度的1.5倍,若陈钢比王昊早出发0.5小时,结果陈钢比王昊晚到0.5小时,求陈钢、王昊两人的行驶速度.【题文】如图,在△ABC中,AB=AC,点M在BA的延长线上. 【题文】为了提高学生的综合素质,某中学成立了以下社团:
【题文】为了提高学生的综合素质,某中学成立了以下社团:| A.机器人, | B.围棋, | C.羽毛球, | D.电影配音.每人只能加入一个社团,为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如图两幅不完整的统计图,其中图(1)中A所占扇形的圆心角为36°. |
 【题文】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=﹣
【题文】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=﹣ 的图象交于二、四象限内的A、B两点,与y轴交于C点,点A的坐标为(m,3),点B与点A关于直线y=x对称.
的图象交于二、四象限内的A、B两点,与y轴交于C点,点A的坐标为(m,3),点B与点A关于直线y=x对称. 【题文】已知,AB是⊙O的
【题文】已知,AB是⊙O的 直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
直径,点C在⊙O上,点P是AB延长线上一点,连接CP. 【题文】如图,抛物线与x轴相交于点A(﹣3,0)、点B(1,0),与y轴交于点C(0,3),点D是抛物线上一动点,联结OD交线段AC于点E.
【题文】如图,抛物线与x轴相交于点A(﹣3,0)、点B(1,0),与y轴交于点C(0,3),点D是抛物线上一动点,联结OD交线段AC于点E.
 ,最高气温是
,最高气温是 ,这一天的温差为( )
,这一天的温差为( )A. | B. | C. | D. |
| A.2 | B.5 | C.4 | D.3 |
 在实数范围内有意义,则x满足的条件是( )
在实数范围内有意义,则x满足的条件是( )A.x≥ | B.x≤ | C.x= | D.x≠ |
 的方程式为
的方程式为 ,直线
,直线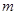 的方程式为
的方程式为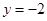 ,将直线
,将直线 和直线
和直线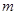 画在平面直角坐标内正确的是()
画在平面直角坐标内正确的是()A. | B. |
C. | D. |
 向上平移3个单位,下列在该平移后的直线上的点是( )
向上平移3个单位,下列在该平移后的直线上的点是( )A. | B. | C. | D. |
A.若a≠b,则 | B.若a>|b|,则a>b |
| C.若|a|=|b|,则a=b | D.若|a|>|b|,则a>b |
 的解是( )
的解是( )A. | B. | C. | D. |

A.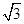 | B.2 | C. | D.4 |
| A.17 | B.19 | C.21 | D.22 |
 ,则
,则 的值为( )
的值为( )| A.5 | B.10 | C.32 | D.64 |

A. | B. | C. | D. |
 、
、 、…、
、…、 十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接
十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接 、
、 、
、 、
、 、
、 ,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
| A.P2 P3 | B.P4 P5 | C.P7 P8 | D.P8 P9 |
 (x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为( )
(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为( )
| A.1 | B.2 | C.3 | D.4 |
 ≈1.414,
≈1.414, ≈1.732,
≈1.732, ≈2.236)( )
≈2.236)( )
| A.320cm | B.395.24 cm | C.431.76 cm | D.480 cm |
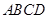 中,点
中,点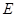 、
、 分别在边
分别在边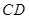 ,
,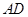 上,
上,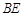 与
与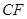 交于点
交于点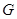 .若
.若 ,
, ,则
,则 的长为( )
的长为( )
A. | B. | C. | D. |
 的结果是
的结果是 【题文】如图,已知正方形
【题文】如图,已知正方形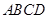 的边长为3,
的边长为3,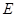 为
为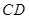 边上一点(不与端点重合),将
边上一点(不与端点重合),将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点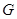 ,连接
,连接 ,
,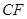 .
.
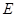 为
为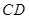 的中点,则
的中点,则 的面积为
的面积为 【题文】下图中是小明完成的一道作业题,请你参考小明的方法解答下面的问题:
【题文】下图中是小明完成的一道作业题,请你参考小明的方法解答下面的问题:
 ;
; .
. ,直接写出
,直接写出 的值.【题文】已知
的值.【题文】已知 ,
, .
. ,并将结果整理成关于
,并将结果整理成关于 的整式;
的整式; 的结果与
的结果与 无关,求
无关,求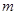 、
、 的值;
的值; 的值.【题文】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
的值.【题文】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:| 组别 | 个数段 | 频数 | 频率 |
| 1 |  | 5 | 0.1 |
| 2 |  | 21 | 0.42 |
| 3 |  | 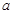 | |
| 4 |  | | 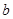 |
 ,
, ;
; 【题文】如图,在五边形
【题文】如图,在五边形 中,
中, ,
, ,
, .
.
 ;
; 时,求
时,求 的度数;
的度数;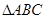 的外心与
的外心与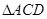 的内心重合,请直接写出
的内心重合,请直接写出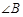 的度数.【题文】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程
的度数.【题文】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程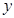 (米)与时间
(米)与时间 (分)的函数关系如图2所示.
(分)的函数关系如图2所示. 
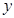 (米)与时间
(米)与时间 (分)的函数表达式.
(分)的函数表达式. 与
与 轴交于点
轴交于点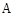 ,与
,与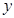 轴交于点
轴交于点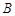 ,抛物线
,抛物线 经过点
经过点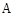 、
、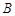 .
.
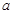 、
、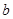 满足的关系式及
满足的关系式及 的值.
的值. 时,若
时,若 的函数值随
的函数值随 的增大而增大,求
的增大而增大,求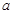 的取值范围.
的取值范围. 时,在抛物线上是否存在点
时,在抛物线上是否存在点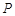 ,使
,使 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点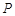 的坐标;若不存在,请说明理由.【题文】已知在扇形
的坐标;若不存在,请说明理由.【题文】已知在扇形 中,圆心角
中,圆心角 ,半径
,半径 .
.
 作
作 ,交弧
,交弧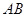 于点
于点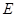 ,再过点
,再过点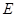 作
作 于点
于点 ,则
,则 的长为_________,
的长为_________, 的度数为_________;
的度数为_________;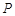 为弧
为弧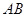 上的动点,过点
上的动点,过点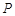 作
作 于点
于点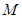 ,
, 于点
于点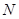 ,点
,点 分别在半径
分别在半径 ,
,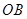 上,连接
上,连接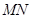 ,则
,则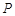 运动的路径长是多少?
运动的路径长是多少?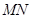 的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;
的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;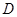 是
是 的外心,直接写出点
的外心,直接写出点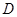 运动的路经长.【题文】-2的倒数是()
运动的路经长.【题文】-2的倒数是()| A.-2 | B. | C. | D.2 |
A. | B. |
C. | D. |
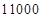 千米,
千米,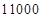 用科学记数法表示是( )
用科学记数法表示是( )A. | B. | C. | D. |
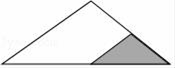
| A.两点确定一条直线 | B.线段是直线的一部分 |
| C.经过一点有无数条直线 | D.两点之间,线段最短 |
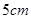 ,母线长为
,母线长为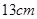 ,则这个圆锥的侧面积是( )
,则这个圆锥的侧面积是( )A. | B. | C. | D. |
 的一元二次方程
的一元二次方程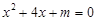 有实数根,则
有实数根,则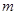 取值范围为( )
取值范围为( )A. | B. | C. | D. |
A.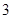 | B. | C. | D.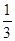 |
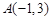 关于
关于 轴的对称点
轴的对称点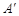 在正比例函数
在正比例函数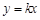 的图象上,则
的图象上,则 的值为( )
的值为( )A.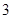 | B.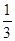 | C. | D. |
| A.正方形 | B.菱形 | C.矩形 | D.以上都不对 |
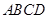 的边长为
的边长为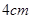 ,动点
,动点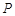 从
从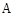 出发,沿
出发,沿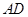 边以
边以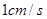 的速度运动,动点
的速度运动,动点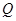 从
从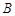 出发,沿
出发,沿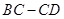 边以
边以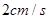 的速度运动,点
的速度运动,点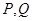 同时出发,运动到点
同时出发,运动到点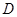 时均停止运动.设运动时间为
时均停止运动.设运动时间为 (单位:
(单位: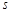 ),
),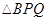 的面积为
的面积为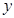 (单位:
(单位: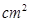 ),则
),则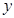 与
与 之间的函数图象大致是( )
之间的函数图象大致是( )
A. | B. | C. | D. |
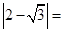
 的外接圆,
的外接圆,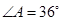 ,则
,则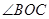 的度数为__________
的度数为__________ .
. 【题文】分解因式:x2-2x+1=
【题文】分解因式:x2-2x+1=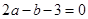 ,则代数式
,则代数式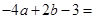 __________.【题文】等腰三角形的底边长为
__________.【题文】等腰三角形的底边长为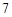 ,腰长是方程
,腰长是方程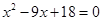 的一个根,则这个等腰三角形的周长为__________.【题文】在平面直角坐标系中,将
的一个根,则这个等腰三角形的周长为__________.【题文】在平面直角坐标系中,将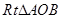 如图放置,直角顶点与原点
如图放置,直角顶点与原点 重合,顶点
重合,顶点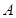 ,
,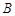 恰好分别落在函数
恰好分别落在函数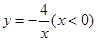 ,
,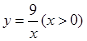 的图象上,则
的图象上,则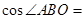 __________.
__________.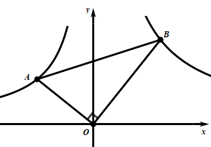 【题文】计算:
【题文】计算: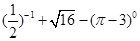 【题文】先化简,再求值:
【题文】先化简,再求值: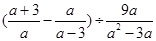 ,其中
,其中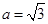 【题文】如图,在
【题文】如图,在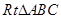 中,
中,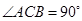 ,
,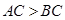 .
.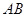 的垂直平分线交
的垂直平分线交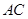 于点
于点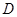 (不要求写作法,但保留作图痕迹);
(不要求写作法,但保留作图痕迹);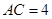 ,
, ,连接
,连接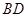 ,求
,求 的周长.
的周长. 【题文】为了调查某小区居民的用水情况,随机抽查了若干个家庭的
【题文】为了调查某小区居民的用水情况,随机抽查了若干个家庭的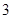 月份用水量,结果如下表:
月份用水量,结果如下表:| 月用水量(立方米) |  |  |  |  |
| 户数 | 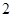 | 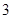 |  | 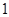 |
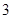 月份平均用水量;
月份平均用水量;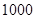 个家庭
个家庭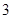 月份总用水量.【题文】如图,在正方形
月份总用水量.【题文】如图,在正方形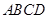 中,
中,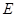 ,
, 分别是
分别是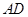 ,
,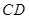 的中点,连接
的中点,连接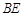 ,
,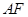 交于点
交于点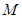 ,分别延长
,分别延长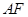 ,
, 交于点
交于点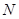 .
.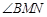 的度数;
的度数;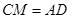 .
. 【题文】 某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
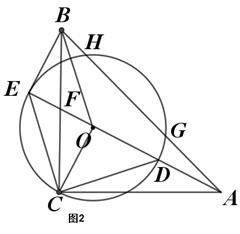
【题文】 某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元. 绕点
绕点 逆时针旋转
逆时针旋转 得
得 ,点
,点 ,
, 分别对应点
分别对应点 ,
, ,且满足
,且满足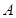 ,
,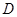 ,
,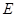 三点在同一条直线上,连接
三点在同一条直线上,连接 交
交 于点
于点 ,
,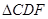 的外接圆圆O与
的外接圆圆O与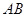 交于
交于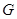 、
、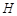
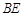 是圆O切线;
是圆O切线;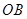 ,
,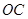 ,若
,若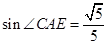 ,判断四边形
,判断四边形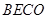 的形状,并说明理由;
的形状,并说明理由;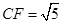 ,求
,求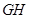 的长.
的长.
 【题文】如图
【题文】如图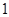 ,在平面直角坐标系中,
,在平面直角坐标系中,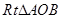 的直角顶点
的直角顶点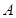 在第一象限,
在第一象限,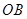 在
在 轴上,且
轴上,且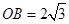 ,
,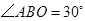 ,
,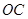 是
是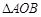 的角平分线.抛物线
的角平分线.抛物线 过点
过点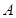 ,
,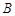 ,点
,点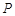 在直线
在直线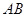 上方的抛物线上,连接
上方的抛物线上,连接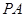 ,
,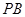 ,
,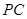 .
.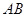 解析式为 ;
解析式为 ;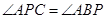 时,求
时,求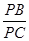 的值;
的值;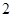 ,作
,作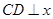 轴于点
轴于点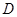 ,连接
,连接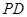 ,若
,若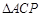 与
与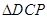 的面积相等,求点
的面积相等,求点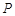 的坐标
的坐标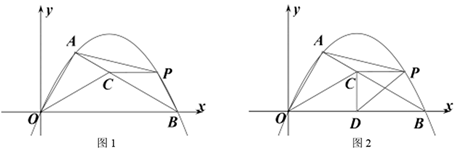 【题文】在﹣4,2,﹣1,3这四个数中,比﹣2小的数是( )
【题文】在﹣4,2,﹣1,3这四个数中,比﹣2小的数是( )| A.﹣4 | B.2 | C.﹣1 | D.3 |
A. | B. | C. | D. |
 ,则
,则 等于( )
等于( )A. | B. | C. | D. |
 是方程组
是方程组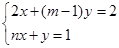 的解,则
的解,则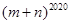 的值为( )
的值为( )A. | B.-1 | C.1 | D.0 |
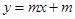 和
和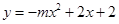 的图象可能是( )
的图象可能是( )A. | B. | C. | D. |
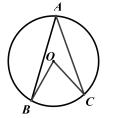
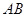 是圆
是圆 的直径,
的直径,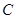 ,
,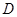 是圆
是圆 上的点,且
上的点,且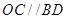 ,
,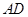 分别与
分别与 ,
,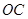 相交于点
相交于点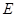 ,
, ,则下列结论:①
,则下列结论:①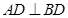 ;②
;②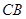 平分
平分 ;③
;③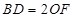 ;④
;④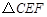 ≌
≌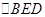 ,其中一定成立的是( )
,其中一定成立的是( )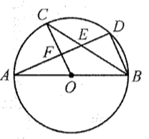
| A.②④ | B.①③④ | C.①②③ | D.①②③④ |
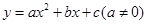 的图象如图,现给出下列结论:①
的图象如图,现给出下列结论:① ;②
;②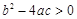 ;③
;③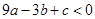 ;④
;④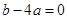 ;⑤
;⑤ 的两个根为
的两个根为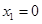 ,
,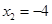 ,其中正确的结论有( )
,其中正确的结论有( )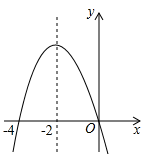
| A.①③④ | B.②④⑤ | C.①②⑤ | D.②③⑤ |
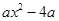 = .【题文】若一个一元二次方程的两个根分别是
= .【题文】若一个一元二次方程的两个根分别是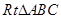 的两条直角边长,且
的两条直角边长,且 ,这个二次方程的二次项系数是1,则常数项是__________.【题文】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折至△AGE,那么△AGE与四边形AECD重叠部分的面积是
,这个二次方程的二次项系数是1,则常数项是__________.【题文】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折至△AGE,那么△AGE与四边形AECD重叠部分的面积是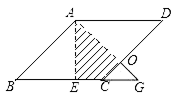 【题文】如图,点C、D在线段AB上,且CD是等腰直角△PCD的底边.当△PDB∽△ACP时(P与A、B与P分别为对应顶点),∠APB=
【题文】如图,点C、D在线段AB上,且CD是等腰直角△PCD的底边.当△PDB∽△ACP时(P与A、B与P分别为对应顶点),∠APB=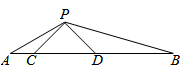 【题文】如图,在
【题文】如图,在 中,AB=AC,BC=4,以
中,AB=AC,BC=4,以 为直径作半圆
为直径作半圆 ,交
,交 于点
于点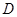 ,则
,则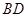 的长是__.
的长是__. 【题文】如图,在平面直角坐标系内,边长为4的等边
【题文】如图,在平面直角坐标系内,边长为4的等边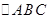 的顶点
的顶点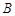 与原点重合,将
与原点重合,将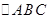 绕顶点
绕顶点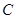 顺时针旋转
顺时针旋转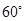 的
的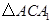 将四边形
将四边形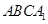 看作一个基本图形,将此基本图形不断复制并平移,则
看作一个基本图形,将此基本图形不断复制并平移,则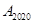 的坐标为__________.
的坐标为__________.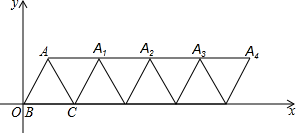 【题文】计算:
【题文】计算: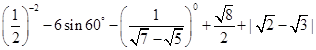 【题文】先化简,再求值:
【题文】先化简,再求值: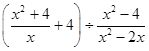 ﹣
﹣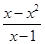 ,然后在0,1,2,3中选一个你认为合适的x值,代入求值.【题文】如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.
,然后在0,1,2,3中选一个你认为合适的x值,代入求值.【题文】如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.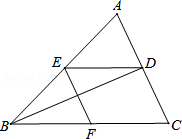 【题文】在一块长16m、宽12m的矩形荒地上,小明要建造一个花园,并使花园所占的面积为荒地面积的一半,其中花园四周小路的宽度都相等,求小路的宽.
【题文】在一块长16m、宽12m的矩形荒地上,小明要建造一个花园,并使花园所占的面积为荒地面积的一半,其中花园四周小路的宽度都相等,求小路的宽.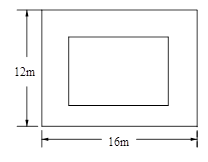 【题文】如图,某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶的仰角为30°,且D离地面的高度DE=5m,坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E、A、C在同一水平线上,求建筑物BC的高.(结果保留整数,参考数据tan50°=1.1918,cos50°=0.6428)
【题文】如图,某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶的仰角为30°,且D离地面的高度DE=5m,坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E、A、C在同一水平线上,求建筑物BC的高.(结果保留整数,参考数据tan50°=1.1918,cos50°=0.6428)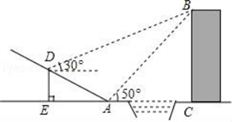 【题文】如图,在平面直角坐标系中,反比例函数
【题文】如图,在平面直角坐标系中,反比例函数 与一次函数
与一次函数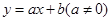 的图象交于
的图象交于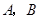 两点,点
两点,点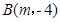 ,
,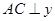 轴于点
轴于点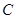 ,
,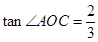 ,
,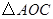 的面积是3,一次函数
的面积是3,一次函数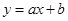 与
与 轴,
轴,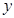 轴分别交于点
轴分别交于点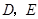 .
.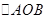 的面积.
的面积. 【题文】如图,
【题文】如图,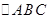 中,
中,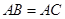 ,以
,以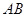 为直径的圆
为直径的圆 与
与 相交于点
相交于点 ,与
,与 的延长线相交于点
的延长线相交于点 ,过点
,过点 作
作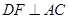 于点
于点
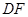 是圆
是圆 的切线;
的切线;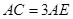 ,
,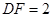 ,求
,求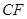 的长.
的长.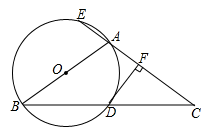 【题文】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图.根据统计图所提供的信息,回答下列问题:
【题文】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图.根据统计图所提供的信息,回答下列问题: ,
, .
.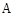 ”类图书的学生约有多少人?
”类图书的学生约有多少人? 【题文】已知:点
【题文】已知:点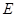 为
为 边上的一个动点.
边上的一个动点.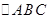 是等边三角形,以
是等边三角形,以 为边在
为边在 的同侧作等边
的同侧作等边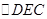 ,连接
,连接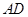 .试比较
.试比较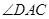 与
与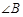 的大小,并说明理由;
的大小,并说明理由;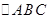 中,
中,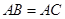 ,以
,以 为底边在
为底边在 的同侧作等腰
的同侧作等腰 ,且
,且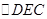 ∽
∽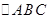 ,连接
,连接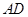 .试判断
.试判断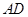 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;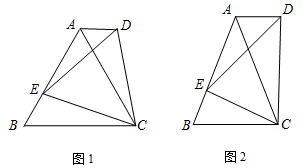 【题文】如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.
【题文】如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.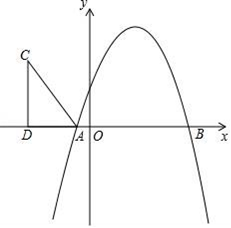 【题文】2018年我国在人工智能领域取得显著成就,自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军,这得益于所建立的大数据中心的规模和数据存储量,它们决定着人工智能深度学习的质量和速度,其中的一个大数据中心能存储58000000000本书籍.将58000000000用科学记数法表示应为( )
【题文】2018年我国在人工智能领域取得显著成就,自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军,这得益于所建立的大数据中心的规模和数据存储量,它们决定着人工智能深度学习的质量和速度,其中的一个大数据中心能存储58000000000本书籍.将58000000000用科学记数法表示应为( )| A.58×109 | B.5.8×1010 | C.5.8×1011 | D.0.58×1011 |
A. | B. | C. | D. |
A. | B. | C. | D. |
A. | B. | C. | D. |
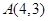 经过某种图形变化后得到点
经过某种图形变化后得到点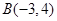 ,这种图形变化可以是()
,这种图形变化可以是()A.关于 轴对称 轴对称 | B.关于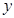 轴对称 轴对称 | C.绕原点逆时针旋转 | D.绕原点顺时针旋转 |
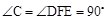 ,
,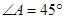 ,
,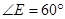 ,点F在CB的延长线上若
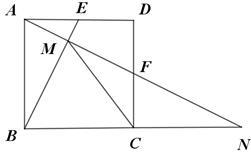
,点F在CB的延长线上若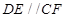 ,则
,则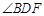 等于( )
等于( )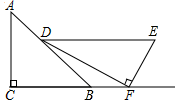
| A.35° | B.25° | C.30° | D.15° |
A. | B. |
C. | D. |
 天数据,整理后绘制成统计表进行分析.
天数据,整理后绘制成统计表进行分析.日均可回收物回收量(千吨) |
|
|
|
|
| 合计 |
频数 | 1 | 2 |
|
| 3 |
|
频率 | 0.05 | 0.10 |
|
| 0.15 | 1 |
 组的频率
组的频率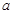 满足
满足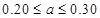 .
.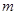 的值为20;
的值为20;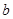 的值可以为7;
的值可以为7;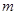 天的日均可回收物回收量的中位数在
天的日均可回收物回收量的中位数在 组;
组;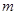 天的日均可回收物回收量的平均数不低于3.
天的日均可回收物回收量的平均数不低于3.| A.①② | B.①③ | C.②③④ | D.①③④ |