 ,坡面长
,坡面长 的斜坡
的斜坡 的底部
的底部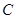 点测得
点测得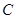 点与塔底
点与塔底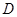 点的距离为
点的距离为 ,此时,李华在坡顶
,此时,李华在坡顶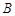 点测得轮毂
点测得轮毂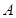 点的仰角
点的仰角 ,请根据测量结果帮他们计算风力发电机塔架
,请根据测量结果帮他们计算风力发电机塔架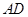 的高度.(结果精确到
的高度.(结果精确到 ,参考数据
,参考数据 ,
, ,
, ,
, ,
, )
)
 ,坡面长
,坡面长 的斜坡
的斜坡 的底部
的底部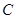 点测得
点测得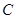 点与塔底
点与塔底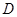 点的距离为
点的距离为 ,此时,李华在坡顶
,此时,李华在坡顶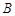 点测得轮毂
点测得轮毂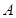 点的仰角
点的仰角 ,请根据测量结果帮他们计算风力发电机塔架
,请根据测量结果帮他们计算风力发电机塔架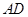 的高度.(结果精确到
的高度.(结果精确到 ,参考数据
,参考数据 ,
, ,
, ,
, ,
, )
)
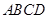 中,
中,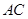 ,
,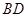 交于点
交于点 ,且
,且 ,
, 的平分线
的平分线 交
交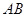 于点
于点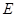 .
.
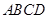 是矩形;
是矩形; ,
, ,求
,求 的长.【题文】越野自行车是中学生喜爱的交通工具,市场巨大,竟争也激烈.某品牌经销商经营的
的长.【题文】越野自行车是中学生喜爱的交通工具,市场巨大,竟争也激烈.某品牌经销商经营的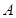 型车去年销售总额为
型车去年销售总额为 万元,今年每辆售价比去年降低
万元,今年每辆售价比去年降低 元,若卖出的数量相同,销售总额将比去年减少
元,若卖出的数量相同,销售总额将比去年减少 .
.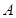 型车每辆销售价为
型车每辆销售价为 元,求
元,求 的值;
的值;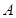 型车和新款
型车和新款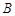 型车共
型车共 辆,且
辆,且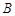 型车的进货数量不超过
型车的进货数量不超过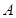 型车数量的两倍,请问应如何安排两种型号车的进货数量,才能使这批售出后获利最多?
型车数量的两倍,请问应如何安排两种型号车的进货数量,才能使这批售出后获利最多?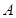 、
、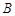 两种型号车今年的进货和销售价格表
两种型号车今年的进货和销售价格表| | 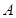 型车 型车 | 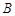 型车 型车 |
| 进货价 |  元/辆 元/辆 |  元/辆 元/辆 |
| 销售价 |  元/辆 元/辆 |  元/辆 元/辆 |
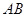 是
是 的直径,
的直径,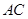 是
是 的切线,连结
的切线,连结 ,过点
,过点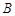 作
作 交
交 于点
于点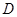 ,延长
,延长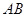 ,
,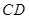 交于点
交于点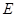 .
.
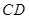 是
是 的切线;
的切线; ,
, ,求
,求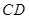 的长.【题文】如图,抛物线
的长.【题文】如图,抛物线 与
与 轴交于点
轴交于点 和点
和点 ,与
,与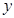 轴交于点
轴交于点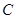 .点
.点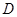 和点
和点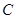 关于
关于 轴对称,点
轴对称,点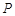 是线段
是线段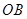 上的一个动点.设点
上的一个动点.设点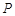 的坐标为
的坐标为 ,过点
,过点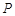 作
作 轴的垂线
轴的垂线 交抛物线于点
交抛物线于点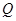 ,交直线
,交直线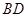 于点
于点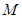 .
.
 ,
, ,当点
,当点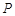 运动到何处时,
运动到何处时, 面积最大?最大面积是多少?并求出此时点
面积最大?最大面积是多少?并求出此时点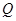 的坐标;
的坐标; 问的前提下,在
问的前提下,在 轴上找一点
轴上找一点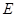 ,使
,使 值最小,求出
值最小,求出 的最小值并直接写出此时点
的最小值并直接写出此时点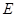 的坐标.【题文】下列图形中,既是轴对称图形又是中心对称图形的有( )
的坐标.【题文】下列图形中,既是轴对称图形又是中心对称图形的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
| A.﹣1 | B.1 | C.3 | D.5 |

| A.122° | B.151° | C.116° | D.97° |
| A.甲稳定 | B.乙稳定 | C.一样稳定 | D.无法比较 |
 cm,一只蚂蚁从点
cm,一只蚂蚁从点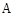 沿圆柱外壁爬到点
沿圆柱外壁爬到点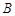 处吃食,要爬行的最短路程是( )
处吃食,要爬行的最短路程是( )
| A.6cm | B.8cm | C.10cm | D.12cm |

| A.y=3x﹣2 | B. | C.y=x﹣1 | D.y=3x﹣3 |

A.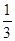 π π | B. π π | C. π π | D. π π |

A. | B. | C. | D. |
 中自变量x的取值范围是
中自变量x的取值范围是 ,则n的值是_____.【题文】已知关于x的方程x2+3x+k2=0的一个根是﹣1,则k=_____.【题文】如图,菱形ABCD的周长为8cm,高AE长为
,则n的值是_____.【题文】已知关于x的方程x2+3x+k2=0的一个根是﹣1,则k=_____.【题文】如图,菱形ABCD的周长为8cm,高AE长为 ,则对角线AC长和BD长之比为
,则对角线AC长和BD长之比为 【题文】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.AB=
【题文】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.AB= ,ON=1,则⊙O的半径长为
,ON=1,则⊙O的半径长为 【题文】如图,已知A(-1,0),B(4,0),C(2,-6)三点,G是线段AC上的动点(不与点A,C重合).若
【题文】如图,已知A(-1,0),B(4,0),C(2,-6)三点,G是线段AC上的动点(不与点A,C重合).若 ABG与
ABG与 ABC相似,点G的坐标____________.
ABC相似,点G的坐标____________. 【题文】某市为治理污水,需要铺设一条全长为550米的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天的工效比原计划增加10%,结果提前5天完成这一任务.假设原计划每天铺设x米,根据题意可列方程为______.【题文】如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFG,对角线AF交边CD于H,连EH.①BE+DH=EH;②若E为BC的中点,则H为CD的中点;③EF平分∠HEC;④
【题文】某市为治理污水,需要铺设一条全长为550米的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天的工效比原计划增加10%,结果提前5天完成这一任务.假设原计划每天铺设x米,根据题意可列方程为______.【题文】如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFG,对角线AF交边CD于H,连EH.①BE+DH=EH;②若E为BC的中点,则H为CD的中点;③EF平分∠HEC;④ .其中正确的序号是_______.
.其中正确的序号是_______. 【题文】先化简,再求值:
【题文】先化简,再求值: ÷(
÷( ﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.【题文】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.【题文】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
 ,求y与x之间的函数关系式.【题文】如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
,求y与x之间的函数关系式.【题文】如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
 【题文】如图,在
【题文】如图,在 ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F. 【题文】“互联网+”时代,网上购物备受消费者青睐.某网店专售一种商品,其成本为每件
【题文】“互联网+”时代,网上购物备受消费者青睐.某网店专售一种商品,其成本为每件 元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于
元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于 .据市场调查发现,月销售量
.据市场调查发现,月销售量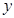 (件)与销售单价
(件)与销售单价 (元)之间的函数关系如表:
(元)之间的函数关系如表:销售单价 (元) (元) | 65 | 70 | 75 | 80 | ··· |
月销售量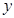 (件) (件) | 475 | 450 | 425 | 400 | ··· |
 请根据表格中所给数据,求出
请根据表格中所给数据,求出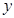 关于
关于 的函数关系式;
的函数关系式; 设该网店每月获得的利润为
设该网店每月获得的利润为 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少? 该网店店主热心公益事业,决定每月从利润中捐出
该网店店主热心公益事业,决定每月从利润中捐出 元资助贫困学生.为了保证捐款后每月利润不低于
元资助贫困学生.为了保证捐款后每月利润不低于 元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?【题文】
元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?【题文】 ABC为等边三角形,以AB边为腰作等腰Rt
ABC为等边三角形,以AB边为腰作等腰Rt ABD,∠BAD=90
ABD,∠BAD=90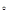 ,AC与BD交于点E,连接CD,过点D作DF⊥BC交BC延长线于点
,AC与BD交于点E,连接CD,过点D作DF⊥BC交BC延长线于点A. (1)如图1,若DF=1,AB= ;AE= ; (2)如图2,将  CDF绕点D顺时针旋转至△C1DF1的位置,点C,F的对应点分别为C1,F1,当DC1平分∠EDC时,DC1与AC交于点M,在AM上取点N,使AN=DM,连接DN,求tan∠NDM的值. CDF绕点D顺时针旋转至△C1DF1的位置,点C,F的对应点分别为C1,F1,当DC1平分∠EDC时,DC1与AC交于点M,在AM上取点N,使AN=DM,连接DN,求tan∠NDM的值.(3)如图3,将  CDF绕点D顺时针旋转至 CDF绕点D顺时针旋转至 C1DF1的位置,点C,F的对应点分别为C1,F1,连接AF1、BC1,点G是BC1的中点,连接A C1DF1的位置,点C,F的对应点分别为C1,F1,连接AF1、BC1,点G是BC1的中点,连接A | B.求 的值; 的值; |
 x2+bx+c经过点A(﹣2,0)、B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0)、B(0、﹣4)与x轴交于另一点C,连接BC. ,求P点坐标.
,求P点坐标. ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由. 【题文】在实数
【题文】在实数 ,
, ,0,
,0, 中,最大的实数是
中,最大的实数是

A. | B.0 | C. | D. |
| A.1.17×107 | B.11.7×106 | C.0.117×107 | D.1.17×108 |

A. | B. | C. | D. |
 )按如图所示方式摆放,使得
)按如图所示方式摆放,使得 ,则
,则 等于( )
等于( )
A. | B.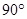 | C. | D. |
| A.等腰直角三角形 | B.正五边形 |
| C.正八边形 | D.平行四边形 |
 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )A. | B. |
C. | D. |
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
| A.平均数 | B.众数 | C.方差 | D.中位数 |
| A.有实数根 | B.有两个不相等的实数根 |
| C.有两个相等的实数根 | D.以上说法都不对 |

| A.25° | B.40° | C.80° | D.100° |
 ,那么函数y=2★x的图象大致是( )
,那么函数y=2★x的图象大致是( )A. | B. | C. | D. |
 【题文】函数y=
【题文】函数y= 中自变量x的取值范围是_____.【题文】如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为
中自变量x的取值范围是_____.【题文】如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为 【题文】若方程组
【题文】若方程组 的解是
的解是 ,则b=_____.【题文】如图,AB是半圆O的直径,且AB=6cm,点C为半圆上的一点,将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是_____.
,则b=_____.【题文】如图,AB是半圆O的直径,且AB=6cm,点C为半圆上的一点,将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是_____. 【题文】如图图形都是由同样大小的正方形“□”按照一定规律排列的,其中图①中共有2个正方形,图②中共有4个正方形,图③中共有7个正方形,图④中共有12个正方形,图⑤中共有21个正方形,……,照此规律排列下去,则图⑩中正方形的个数为_____.
【题文】如图图形都是由同样大小的正方形“□”按照一定规律排列的,其中图①中共有2个正方形,图②中共有4个正方形,图③中共有7个正方形,图④中共有12个正方形,图⑤中共有21个正方形,……,照此规律排列下去,则图⑩中正方形的个数为_____. 【题文】计算:
【题文】计算: .【题文】已知2a2+3a-6=0.求代数式3a(2a+1)-(2a+1)(2a-1)的值.【题文】陈钢和王昊两人从甲市开车前往乙市,甲、乙两市的行驶路程为180千米.已知王昊行驶速度是陈钢行驶速度的1.5倍,若陈钢比王昊早出发0.5小时,结果陈钢比王昊晚到0.5小时,求陈钢、王昊两人的行驶速度.【题文】如图,在△ABC中,AB=AC,点M在BA的延长线上.
.【题文】已知2a2+3a-6=0.求代数式3a(2a+1)-(2a+1)(2a-1)的值.【题文】陈钢和王昊两人从甲市开车前往乙市,甲、乙两市的行驶路程为180千米.已知王昊行驶速度是陈钢行驶速度的1.5倍,若陈钢比王昊早出发0.5小时,结果陈钢比王昊晚到0.5小时,求陈钢、王昊两人的行驶速度.【题文】如图,在△ABC中,AB=AC,点M在BA的延长线上. 【题文】为了提高学生的综合素质,某中学成立了以下社团:
【题文】为了提高学生的综合素质,某中学成立了以下社团:| A.机器人, | B.围棋, | C.羽毛球, | D.电影配音.每人只能加入一个社团,为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如图两幅不完整的统计图,其中图(1)中A所占扇形的圆心角为36°. |
 【题文】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=﹣
【题文】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=﹣ 的图象交于二、四象限内的A、B两点,与y轴交于C点,点A的坐标为(m,3),点B与点A关于直线y=x对称.
的图象交于二、四象限内的A、B两点,与y轴交于C点,点A的坐标为(m,3),点B与点A关于直线y=x对称. 【题文】已知,AB是⊙O的
【题文】已知,AB是⊙O的 直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
直径,点C在⊙O上,点P是AB延长线上一点,连接CP. 【题文】如图,抛物线与x轴相交于点A(﹣3,0)、点B(1,0),与y轴交于点C(0,3),点D是抛物线上一动点,联结OD交线段AC于点E.
【题文】如图,抛物线与x轴相交于点A(﹣3,0)、点B(1,0),与y轴交于点C(0,3),点D是抛物线上一动点,联结OD交线段AC于点E.
 ,最高气温是
,最高气温是 ,这一天的温差为( )
,这一天的温差为( )A. | B. | C. | D. |
| A.2 | B.5 | C.4 | D.3 |
 在实数范围内有意义,则x满足的条件是( )
在实数范围内有意义,则x满足的条件是( )A.x≥ | B.x≤ | C.x= | D.x≠ |
 的方程式为
的方程式为 ,直线
,直线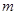 的方程式为
的方程式为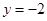 ,将直线
,将直线 和直线
和直线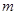 画在平面直角坐标内正确的是()
画在平面直角坐标内正确的是()A. | B. |
C. | D. |
 向上平移3个单位,下列在该平移后的直线上的点是( )
向上平移3个单位,下列在该平移后的直线上的点是( )A. | B. | C. | D. |
A.若a≠b,则 | B.若a>|b|,则a>b |
| C.若|a|=|b|,则a=b | D.若|a|>|b|,则a>b |
 的解是( )
的解是( )A. | B. | C. | D. |

A.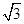 | B.2 | C. | D.4 |
| A.17 | B.19 | C.21 | D.22 |
 ,则
,则 的值为( )
的值为( )| A.5 | B.10 | C.32 | D.64 |

A. | B. | C. | D. |
 、
、 、…、
、…、 十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接
十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接 、
、 、
、 、
、 、
、 ,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
| A.P2 P3 | B.P4 P5 | C.P7 P8 | D.P8 P9 |
 (x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为( )
(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为( )
| A.1 | B.2 | C.3 | D.4 |
 ≈1.414,
≈1.414, ≈1.732,
≈1.732, ≈2.236)( )
≈2.236)( )
| A.320cm | B.395.24 cm | C.431.76 cm | D.480 cm |
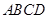 中,点
中,点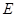 、
、 分别在边
分别在边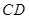 ,
,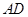 上,
上,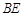 与
与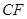 交于点
交于点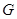 .若
.若 ,
, ,则
,则 的长为( )
的长为( )
A. | B. | C. | D. |
 的结果是
的结果是 【题文】如图,已知正方形
【题文】如图,已知正方形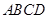 的边长为3,
的边长为3,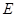 为
为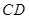 边上一点(不与端点重合),将
边上一点(不与端点重合),将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点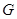 ,连接
,连接 ,
,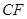 .
.
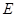 为
为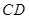 的中点,则
的中点,则 的面积为
的面积为 【题文】下图中是小明完成的一道作业题,请你参考小明的方法解答下面的问题:
【题文】下图中是小明完成的一道作业题,请你参考小明的方法解答下面的问题:
 ;
; .
. ,直接写出
,直接写出 的值.【题文】已知
的值.【题文】已知 ,
, .
. ,并将结果整理成关于
,并将结果整理成关于 的整式;
的整式; 的结果与
的结果与 无关,求
无关,求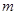 、
、 的值;
的值; 的值.【题文】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
的值.【题文】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:| 组别 | 个数段 | 频数 | 频率 |
| 1 |  | 5 | 0.1 |
| 2 |  | 21 | 0.42 |
| 3 |  | 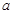 | |
| 4 |  | | 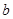 |
 ,
, ;
; 【题文】如图,在五边形
【题文】如图,在五边形 中,
中, ,
, ,
, .
.
 ;
; 时,求
时,求 的度数;
的度数;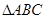 的外心与
的外心与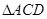 的内心重合,请直接写出
的内心重合,请直接写出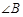 的度数.【题文】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程
的度数.【题文】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程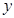 (米)与时间
(米)与时间 (分)的函数关系如图2所示.
(分)的函数关系如图2所示. 
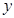 (米)与时间
(米)与时间 (分)的函数表达式.
(分)的函数表达式. 与
与 轴交于点
轴交于点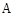 ,与
,与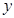 轴交于点
轴交于点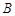 ,抛物线
,抛物线 经过点
经过点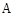 、
、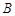 .
.
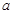 、
、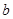 满足的关系式及
满足的关系式及 的值.
的值. 时,若
时,若 的函数值随
的函数值随 的增大而增大,求
的增大而增大,求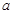 的取值范围.
的取值范围. 时,在抛物线上是否存在点
时,在抛物线上是否存在点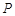 ,使
,使 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点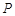 的坐标;若不存在,请说明理由.【题文】已知在扇形
的坐标;若不存在,请说明理由.【题文】已知在扇形 中,圆心角
中,圆心角 ,半径
,半径 .
.
 作
作 ,交弧
,交弧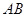 于点
于点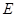 ,再过点
,再过点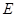 作
作 于点
于点 ,则
,则 的长为_________,
的长为_________, 的度数为_________;
的度数为_________;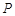 为弧
为弧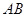 上的动点,过点
上的动点,过点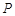 作
作 于点
于点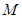 ,
, 于点
于点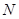 ,点
,点 分别在半径
分别在半径 ,
,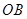 上,连接
上,连接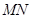 ,则
,则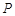 运动的路径长是多少?
运动的路径长是多少?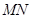 的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;
的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;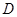 是
是 的外心,直接写出点
的外心,直接写出点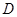 运动的路经长.【题文】-2的倒数是()
运动的路经长.【题文】-2的倒数是()| A.-2 | B. | C. | D.2 |
A. | B. |
C. | D. |
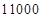 千米,
千米,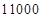 用科学记数法表示是( )
用科学记数法表示是( )A. | B. | C. | D. |
| A.两点确定一条直线 | B.线段是直线的一部分 |
| C.经过一点有无数条直线 | D.两点之间,线段最短 |
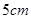 ,母线长为
,母线长为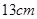 ,则这个圆锥的侧面积是( )
,则这个圆锥的侧面积是( )A. | B. | C. | D. |
 的一元二次方程
的一元二次方程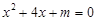 有实数根,则
有实数根,则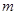 取值范围为( )
取值范围为( )A. | B. | C. | D. |
A.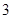 | B. | C. | D.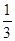 |
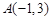 关于
关于 轴的对称点
轴的对称点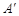 在正比例函数
在正比例函数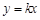 的图象上,则
的图象上,则 的值为( )
的值为( )A.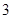 | B.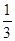 | C. | D. |
| A.正方形 | B.菱形 | C.矩形 | D.以上都不对 |
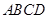 的边长为
的边长为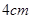 ,动点
,动点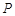 从
从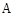 出发,沿
出发,沿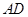 边以
边以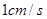 的速度运动,动点
的速度运动,动点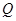 从
从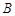 出发,沿
出发,沿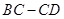 边以
边以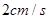 的速度运动,点
的速度运动,点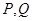 同时出发,运动到点
同时出发,运动到点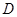 时均停止运动.设运动时间为
时均停止运动.设运动时间为 (单位:
(单位: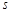 ),
),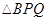 的面积为
的面积为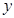 (单位:
(单位: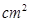 ),则
),则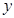 与
与 之间的函数图象大致是( )
之间的函数图象大致是( )
A. | B. | C. | D. |
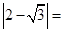
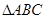 的外接圆,
的外接圆,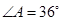 ,则
,则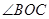 的度数为__________
的度数为__________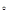 .
. 【题文】分解因式:x2-2x+1=
【题文】分解因式:x2-2x+1=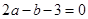 ,则代数式
,则代数式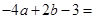 __________.【题文】等腰三角形的底边长为
__________.【题文】等腰三角形的底边长为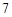 ,腰长是方程
,腰长是方程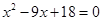 的一个根,则这个等腰三角形的周长为__________.【题文】在平面直角坐标系中,将
的一个根,则这个等腰三角形的周长为__________.【题文】在平面直角坐标系中,将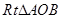 如图放置,直角顶点与原点
如图放置,直角顶点与原点 重合,顶点
重合,顶点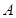 ,
,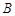 恰好分别落在函数
恰好分别落在函数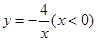 ,
,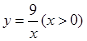 的图象上,则
的图象上,则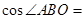 __________.
__________.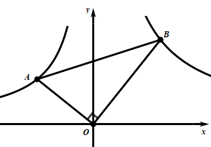 【题文】计算:
【题文】计算: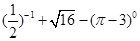 【题文】先化简,再求值:
【题文】先化简,再求值: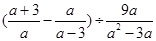 ,其中
,其中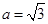 【题文】如图,在
【题文】如图,在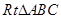 中,
中,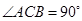 ,
,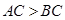 .
.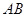 的垂直平分线交
的垂直平分线交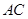 于点
于点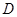 (不要求写作法,但保留作图痕迹);
(不要求写作法,但保留作图痕迹);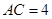 ,
, ,连接
,连接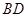 ,求
,求 的周长.
的周长. 【题文】为了调查某小区居民的用水情况,随机抽查了若干个家庭的
【题文】为了调查某小区居民的用水情况,随机抽查了若干个家庭的 月份用水量,结果如下表:
月份用水量,结果如下表:| 月用水量(立方米) |  |  |  |  |
| 户数 |  |  |  |  |
 月份平均用水量;
月份平均用水量;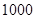 个家庭
个家庭 月份总用水量.
月份总用水量.